2020年8月11日更新
はじめに
本稿では，等分布荷重を受ける片持ちはりのせん断力図（SFD），曲げモーメント図（BMD），たわみ曲線を MATLAB・Octave により計算し，グラフ化する方法について述べる。
概要
等分布荷重*1を受ける片持ちはり*2（cantilever）の
- せん断力（shearing force）
- 曲げモーメント（bending moment）
- たわみ（deflection）
を計算する。
計算結果に基づき，同プログラムでは，
- せん断力図（SFD : Shearing Force Diagram）
- 曲げモーメント図（BMD : Bending Moment Diagram）
- たわみ曲線（deflection curve）
のグラフを描画する。
等分布荷重を受ける片持ちはりの「せん断力」「曲げモーメント」「たわみ」の計算過程，グラフの説明は，［わかりやすい・詳細］等分布荷重を受ける片持はりのたわみでわかりやすく，そして詳細に解説する。
検討モデル
等分布荷重を受ける片持ちはりのせん断力，曲げモーメント，たわみを検討するモデルを下図に示す。
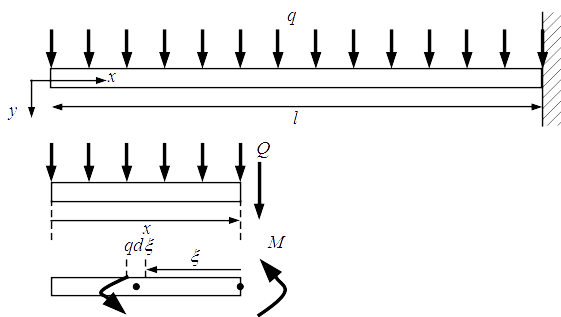
片持ちはりは，回転も移動もできない固定支点で支持される。
はりの先端を $xy$ 座標の原点とし，$x$ については固定支持方向を正，$y$ については鉛直下向きを正とする。
また，はりの長さは $l$ とし，想定する荷重 $w(x)$ は単位長さ当たり $q$ の等分布荷重とする。
プログラムのソースコード
xx=0:1:1000;
ll=1000;%[mm]
qq=0.1;%[N/mm]
EE=200000;%[N/mm2]
Iz=3000;%[mm4]
Qx=-qq*xx;
Mx=-qq/2*xx.^2;
yx=qq/24/EE/Iz*(xx.^4-4*ll^3*xx+3*ll^4);
figure(1);%せん断力図
plot(xx,Qx);
xlabel('x [mm]');ylabel('shearing force [N]');
figure(2);%曲げモーメント
plot(xx,Mx);
xlabel('x [mm]');ylabel('bending moment [N・mm]');
figure(3);%たわみ
plot(xx,yx);
xlabel('x [mm]');ylabel('y [mm]');
設定条件
等分布荷重 0.1 [N/mm] を受ける片持ちはり（長さ 1,000 [mm]）のせん断力，曲げモーメント，たわみを計算している。
なお，たわみについては，片持ちはりの縦弾性係数 200,000 [N/mm2]，断面二次モーメント 3,000 [mm4] として計算している。
グラフの説明
本プログラムで出力した SFD，BMD，たわみ曲線のグラフを示す。
せん断力図（SFD）
はりを先端から長さ $x$ の位置で切断すると，長さ $x$ の部分には大きさ $qx$ の荷重が下向きに作用し，これが右側断面に作用するせん断力 $Q$ とつり合っている。
\[ Q=-qx \]
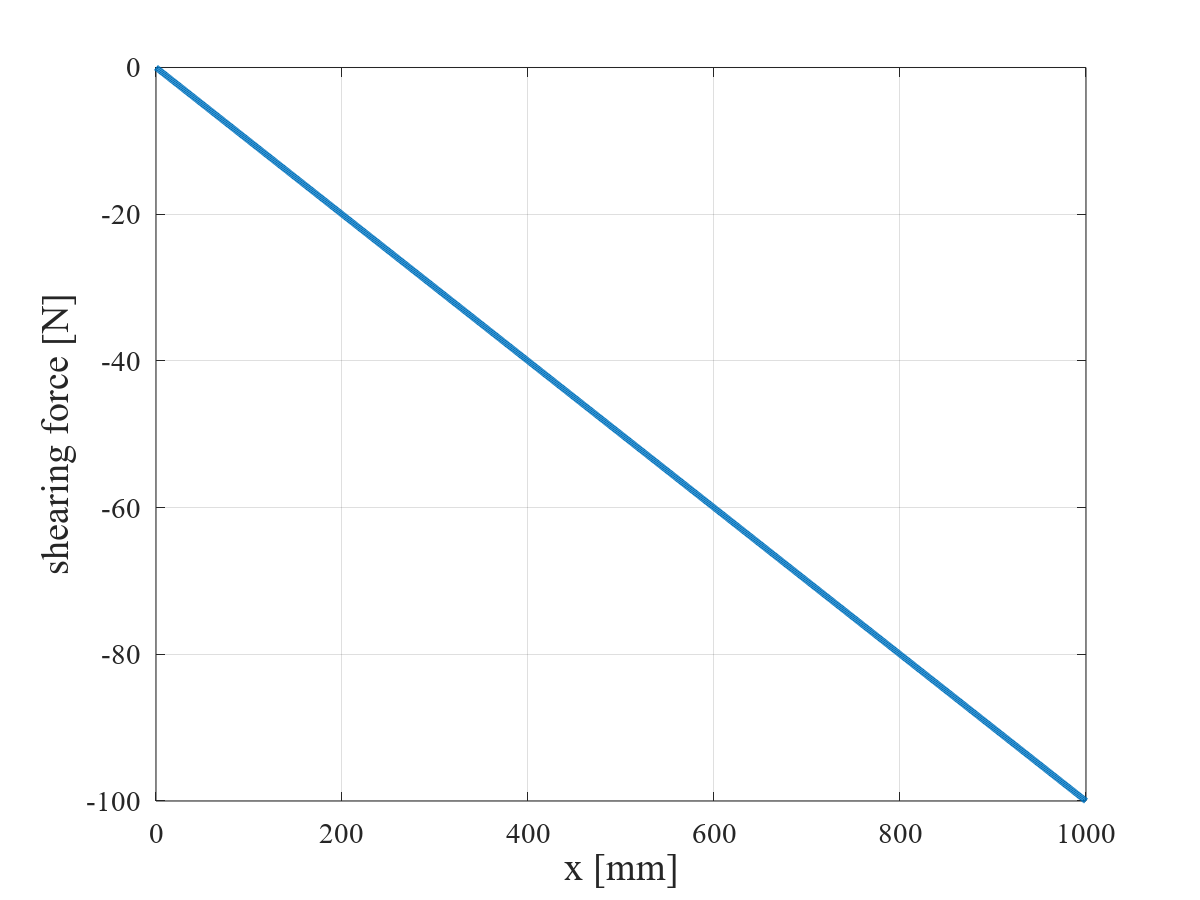
等分布荷重を受ける片持ちはりのせん断力図（SFD）を下図に示す。
せん断力は，単純減少する。
曲げモーメント図（BMD）
曲げモーメント $M$ は次式で与えられる。
\[ M=-\frac{q^2}{2}x^2 \]
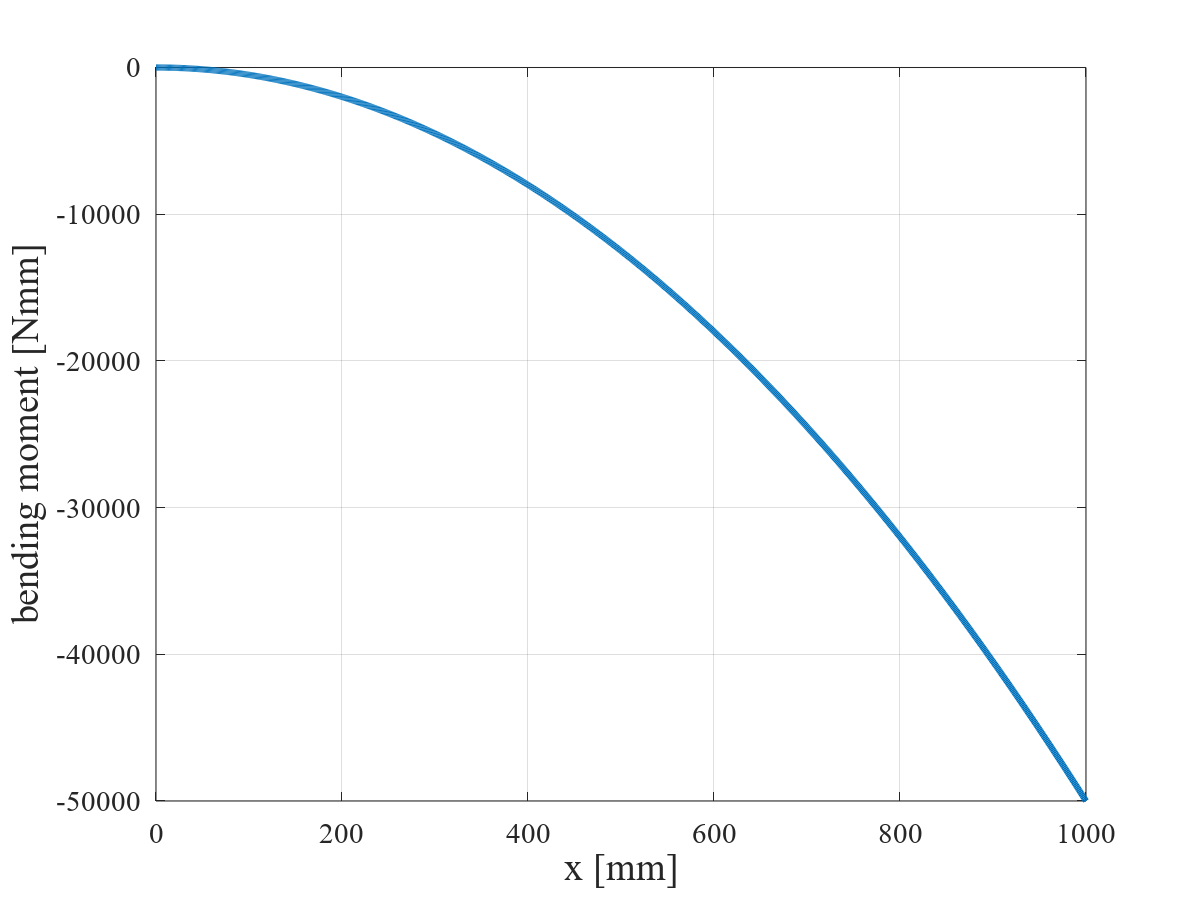
等分布荷重を受ける片持ちはりの曲げモーメント図を下図に示す。
曲げモーメントは，二次関数で単純減少する。
たわみ曲線
たわみ $y$ は次式で与えられる。
\[ y(x)=\frac{q}{24EI_z}(x^4-4l^3x+3l^4) \]
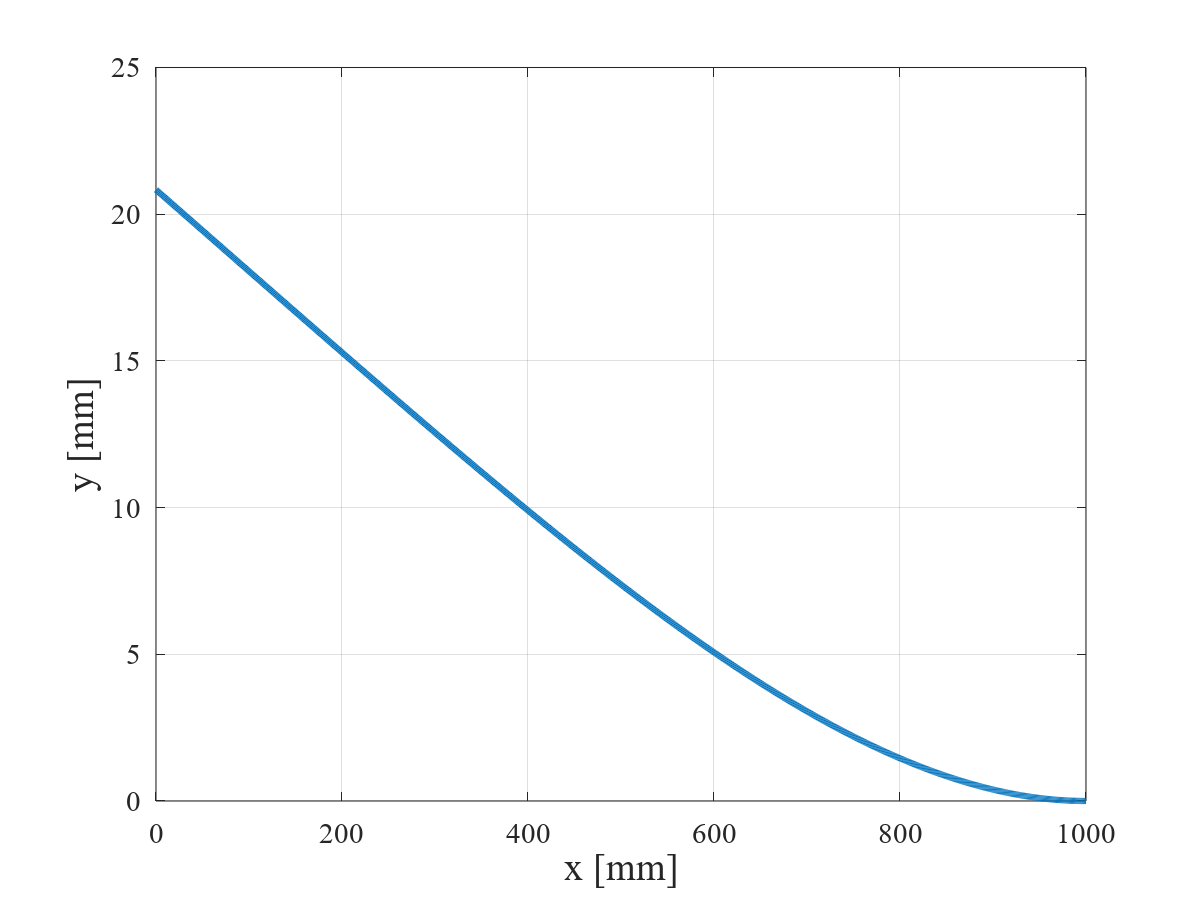
等分布荷重を受ける片持ちはりのたわみ曲線を下図に示す。
たわみ曲線は，四次関数で単純減少し，片持ちはりの支持点ではたわみとたわみの傾きは 0 となる。
